Tensors and Relativity: Assignment 6

Peter Dunsby Room 310a Applied Mathematics

• (1) Consider the integral

  

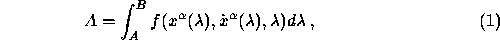
  evaluated along some path 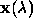connecting fixed points A and B in spacetime. Here f is regarded as a function of 8 independent variables 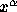and 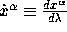. By varying the path 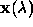, show that A is extremized for

  

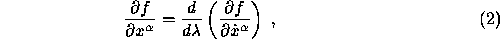
  where 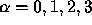. These are the Euler- Lagrange equations.

• (2) Prove that the geodesic equation

  

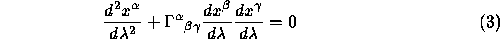
  holds for any parameter 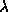along the curve such that 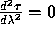, being the proper time measured along the curve.

  Hint!

• (3) Using the usual coordinate transformations from Cartesian to spherical polars, calculate the metric on the surface of a sphere of unit radius. Find the inverse metric.

  Hint!

• (4) Calculate the Riemann curvature tensor of the surface of a sphere of unit radius using the result of the previous problem.

  [ Note that in two dimensions the Riemann tensor has only one independent component, so calculate 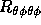and obtain all other components in terms of it.]

  Hint!

• (5) Calculate the Riemann curvature tensor of the surface of a cylinder. You should find that it is flat.

  Hint!

• (6a) Show that covariant differentiation obeys the usual product rule,

  

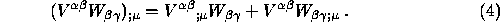
  (6b) Prove that

  

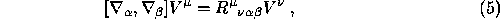
  where .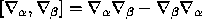

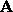  Hint!

• (7) Show that if and 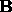are parallel- transported along a curve, then 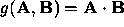is constant along the curve. Deduce that a geodesic that is spacelike/timelike/null somewhere, remains so everywhere.

  Hint!

If you have any problems please come and see me or contact me by email.